Understanding the Cartesian Coordinate System: A Key Concept in Mathematics

Introduction to the Cartesian Coordinate System

The Cartesian coordinate system, an essential concept in mathematics, provides a framework for representing geometric shapes, algebraic equations, and various physical phenomena in a two-dimensional space. Developed by the French mathematician and philosopher René Descartes in the early 17th century, this system revolutionized the field of mathematics by bridging algebra and geometry. Descartes’ innovative approach of using pairs of numbers to signify points on a plane allows for a coherent visual representation of mathematical relationships.

The Cartesian coordinate system is a mathematical framework used to describe the position of points in space using numerical coordinates. While the system can be extended to any number of dimensions—such as four or more in advanced mathematics and physics—we typically focus on two-dimensional (2D) and three-dimensional (3D) spaces for most practical applications in geometry, engineering, physics, and computer graphics.

A two-dimensional space involves flat surfaces—like a sheet of paper—where each point has length and width, but no depth. A three-dimensional space adds an additional component: depth, allowing the representation of real-world volumes and objects.

Two-Dimensional Cartesian Plane

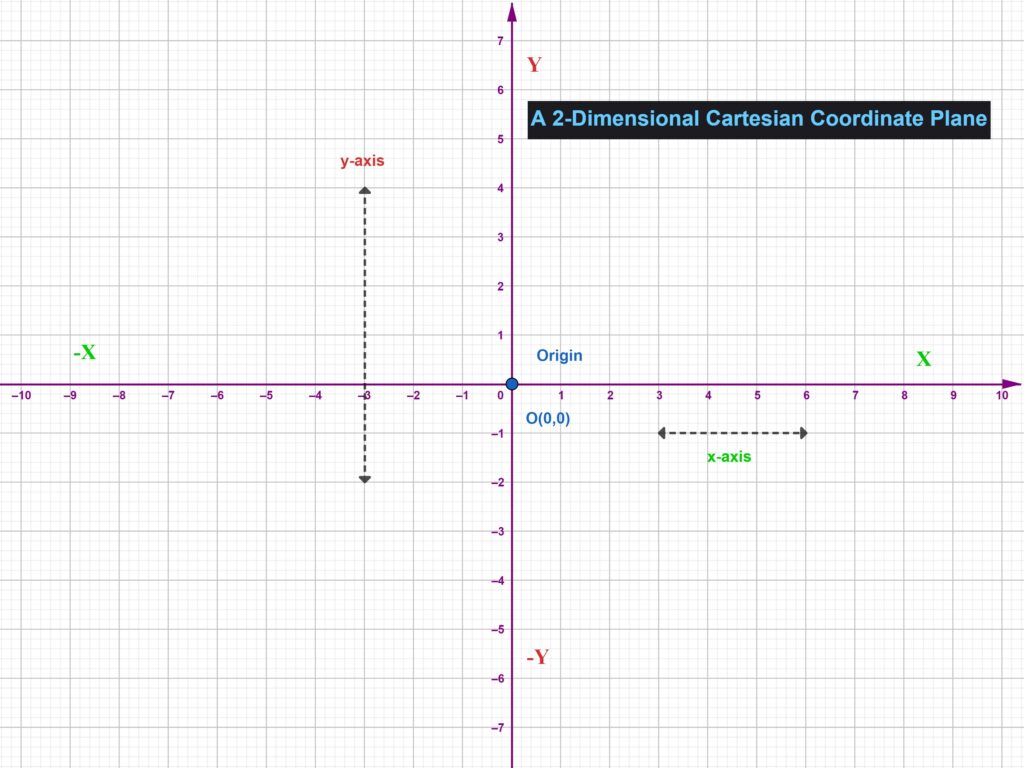
In 2D, the Cartesian plane is defined by two perpendicular number lines: the x-axis (horizontal) and the y-axis (vertical). These axes intersect at the origin, denoted by the point (0, 0). Every point on this plane can be located using an ordered pair (x, y), where:

• x is the distance from the y-axis (left or right),
• y is the distance from the x-axis (up or down).

This system provides a simple and powerful way to graph equations, plot points, and study relationships between variables—laying the groundwork for fields such as algebra, geometry, and calculus.

Three-Dimensional Cartesian Space

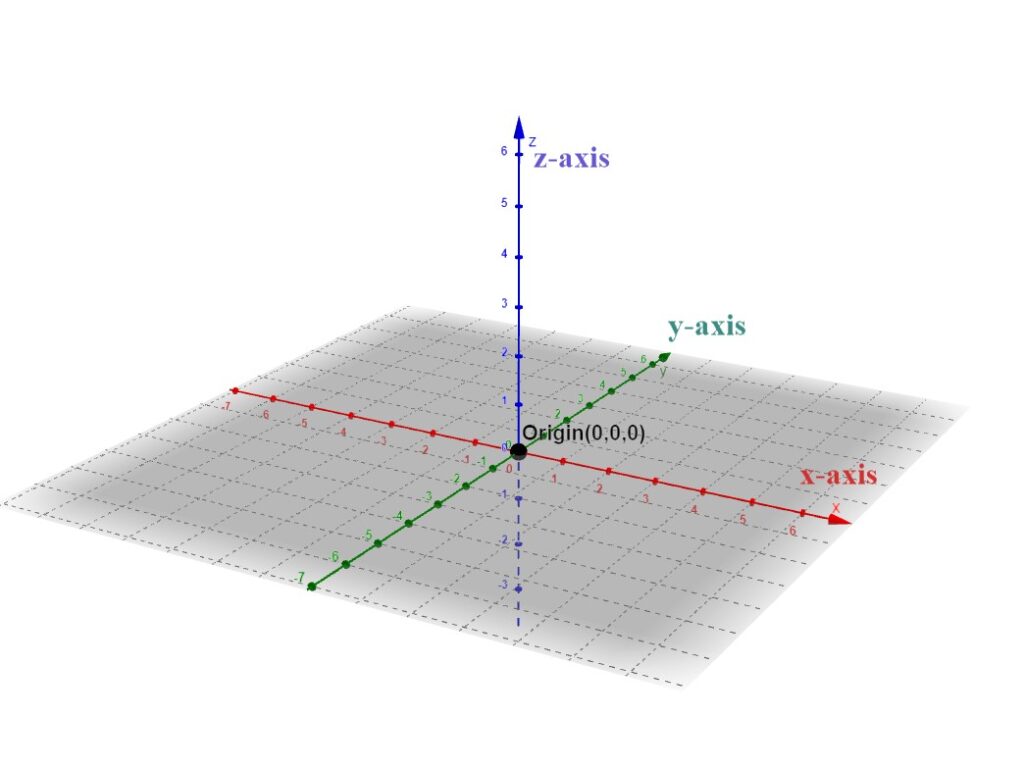
In 3D, a third axis is introduced: the z-axis, which is perpendicular to both the x- and y-axes. The x-, y-, and z-axes intersect at the origin, now represented as (0, 0, 0). Each point in this space is identified by an ordered triplet (x, y, z), where:

• x represents horizontal distance,
• y represents depth or lateral position,
• z represents vertical height.

This three-dimensional Cartesian coordinate system enables us to model and analyze physical space, geometric solids, engineering designs, and more. It is essential in disciplines such as physics, architecture, robotics, and computer-aided design (CAD), where understanding the structure and position of objects in space is crucial.

Moreover, the significance of the Cartesian coordinate system extends beyond mathematics into various fields, such as computer graphics, engineering, and economics. In computer graphics, for instance, the Cartesian system aids in modeling spaces and rendering images, while in engineering, it assists in analyzing structures and motion. Additionally, in economics and data analysis, the Cartesian plane is utilized to graph functions and develop visual representations of data correlations. Through its widespread application, the Cartesian coordinate system remains a vital tool for researchers and professionals seeking to interpret complex information graphically.

The Fundamental Components

Two-Dimensional Cartesian Coordinate System

The Cartesian coordinate system forms a foundational aspect of mathematics, providing a framework for graphically representing and analyzing relationships between numerical values. At its core, the system comprises two primary axes: the x-axis and the y-axis. These axes are perpendicular to each other and intersect at a point known as the origin, which occupies the coordinates (0,0). This intersection not only signifies the starting point for the coordinate system but also serves as a critical reference for measuring distance and direction in the two-dimensional plane.

The x-axis runs horizontally, extending infinitely in both the positive and negative directions. Positive values on the x-axis are located to the right of the origin, while negative values are positioned to the left. Conversely, the y-axis is oriented vertically, extending upwards for positive values and downwards for negative values, also diverging from the origin. Together, these axes create a grid-like structure known as a Cartesian plane, allowing for precise plotting of points determined by their coordinate pairs (x,y).

Another essential aspect of the Cartesian coordinate system is the division of the plane into four distinct quadrants, each denoted by their position relative to the axes. Quadrant I encompasses positive x and positive y values, whereas Quadrant II contains negative x and positive y values. Quadrant III features negative values for both axes, and Quadrant IV is characterized by positive x and negative y values. This quadrant organization aids in classifying points based on their coordinates, facilitating tasks such as graphing functions or solving equations.

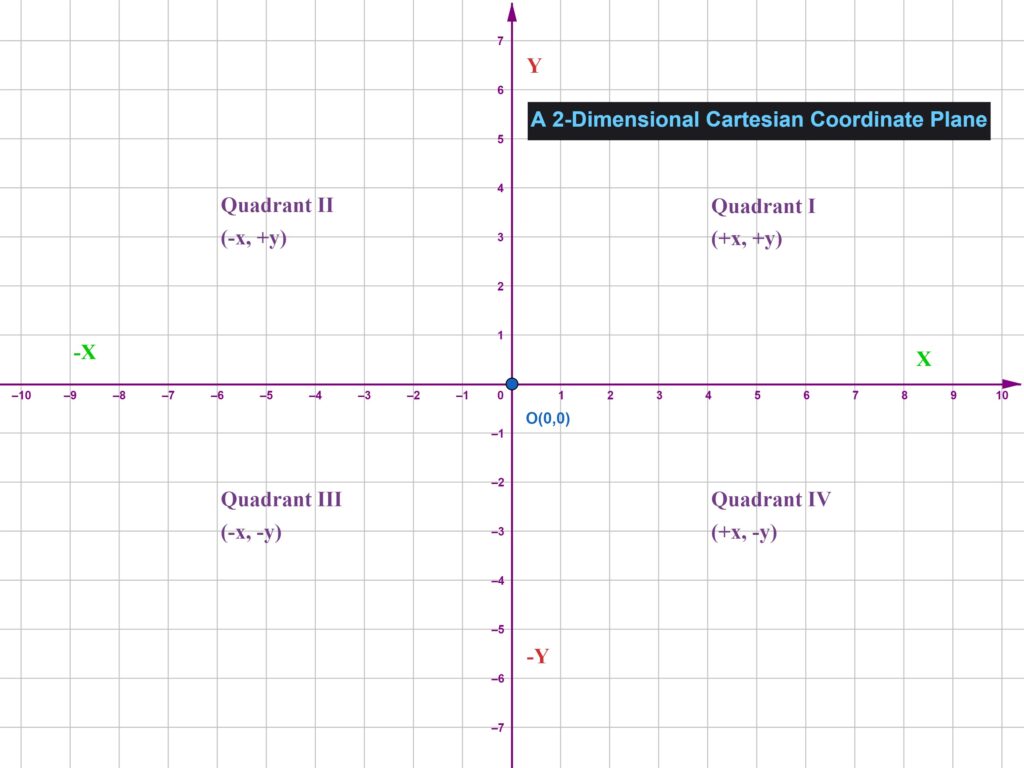
Overall, the x-axis, y-axis, and the resulting quadrants are fundamental components of the Cartesian coordinate system, integral to visualizing relationships between variables in mathematics. Understanding these elements is crucial for mastering more advanced mathematical concepts, whether in algebra, geometry, or calculus.

Three-Dimensional Cartesian Coordinate System

The Cartesian coordinate system is a foundational concept in mathematics, providing a framework for graphically representing and analyzing relationships between numerical values in space. In three dimensions, the system consists of three primary axes: the x-axis, y-axis, and z-axis. Each axis is perpendicular to the other two, and all three intersect at a single point known as the origin, which occupies the coordinates (0, 0, 0). This intersection marks the starting point for the coordinate system and serves as a crucial reference for measuring distance and direction within three-dimensional space.

The x-axis extends horizontally, running infinitely in both the positive (right) and negative (left) directions relative to the origin. The y-axis typically extends in depth, moving forward for positive values and backward for negative values. The z-axis is oriented vertically, with positive values extending upward from the origin and negative values extending downward. Together, these three mutually perpendicular axes form a three-dimensional grid-like structure known as the Cartesian space, which enables the precise plotting of points using coordinate triplets (x, y, z). Here, x, y, and z represent distances from the respective yz-plane, xz-plane, and xy-plane.

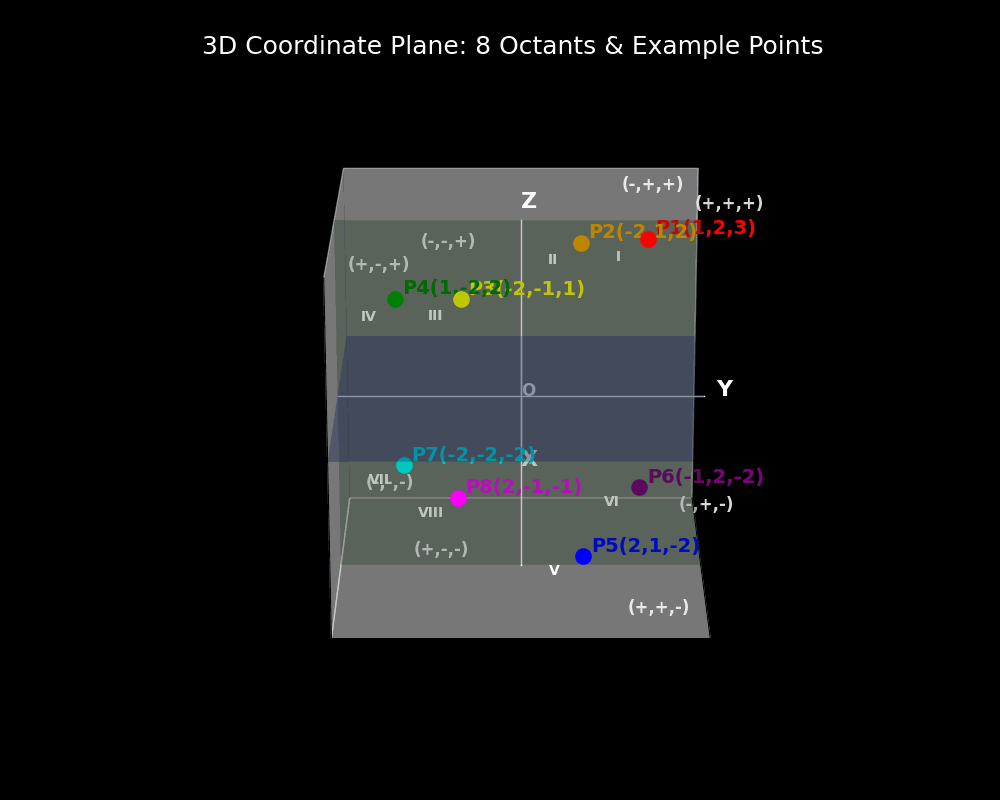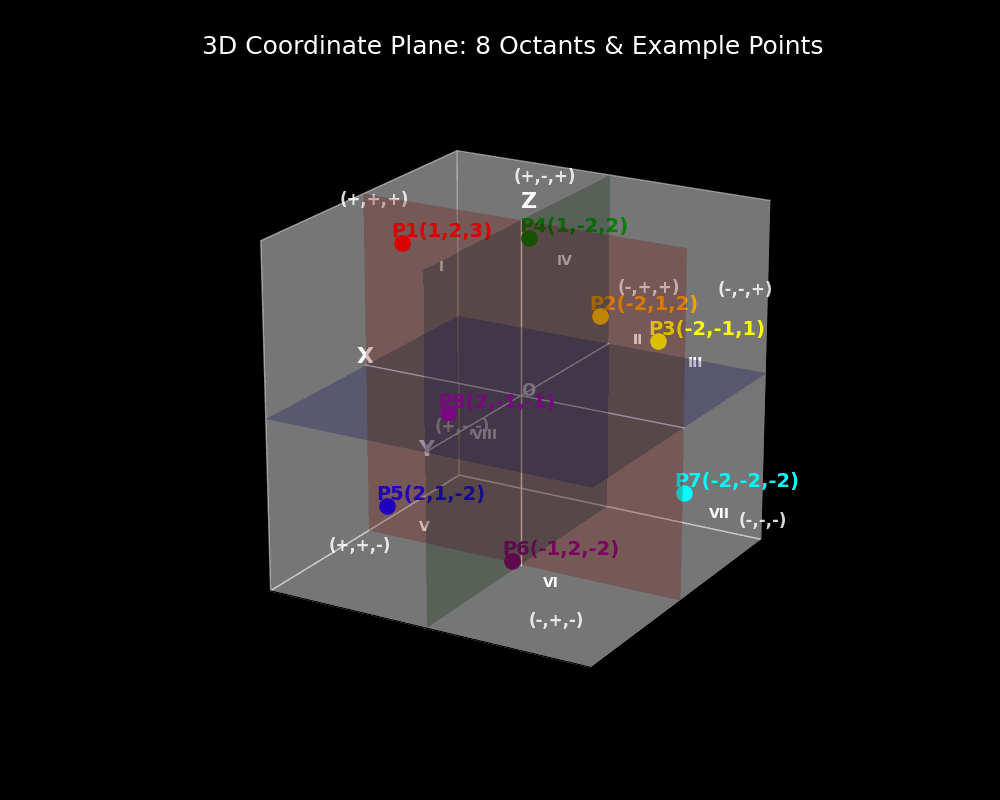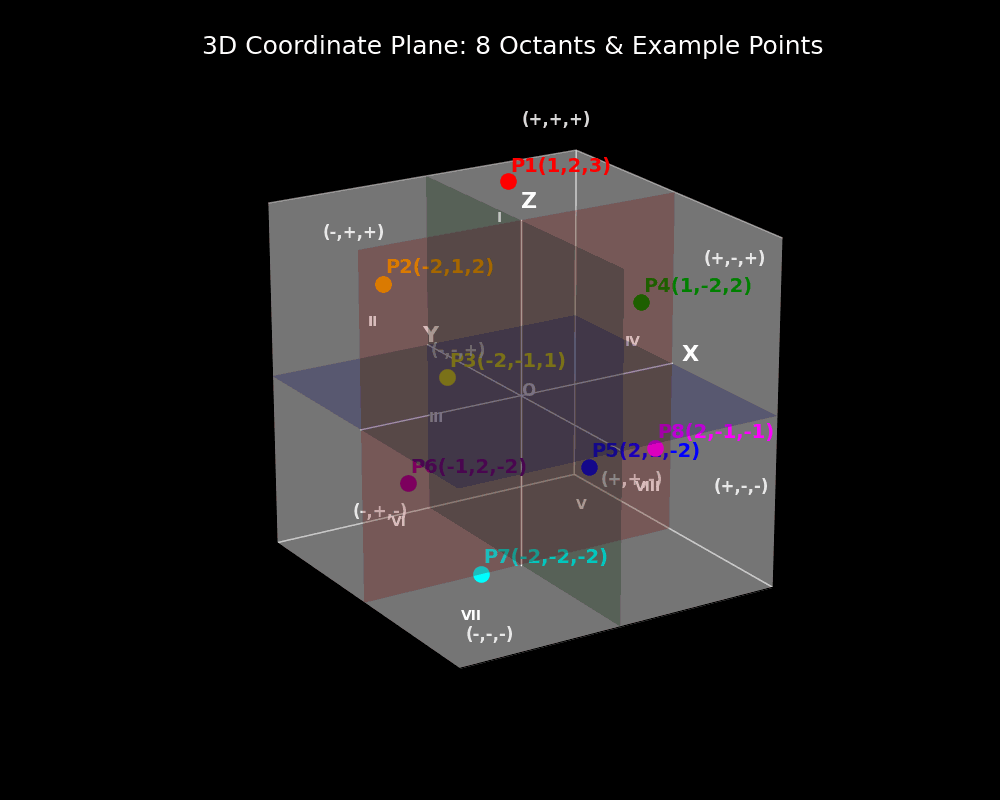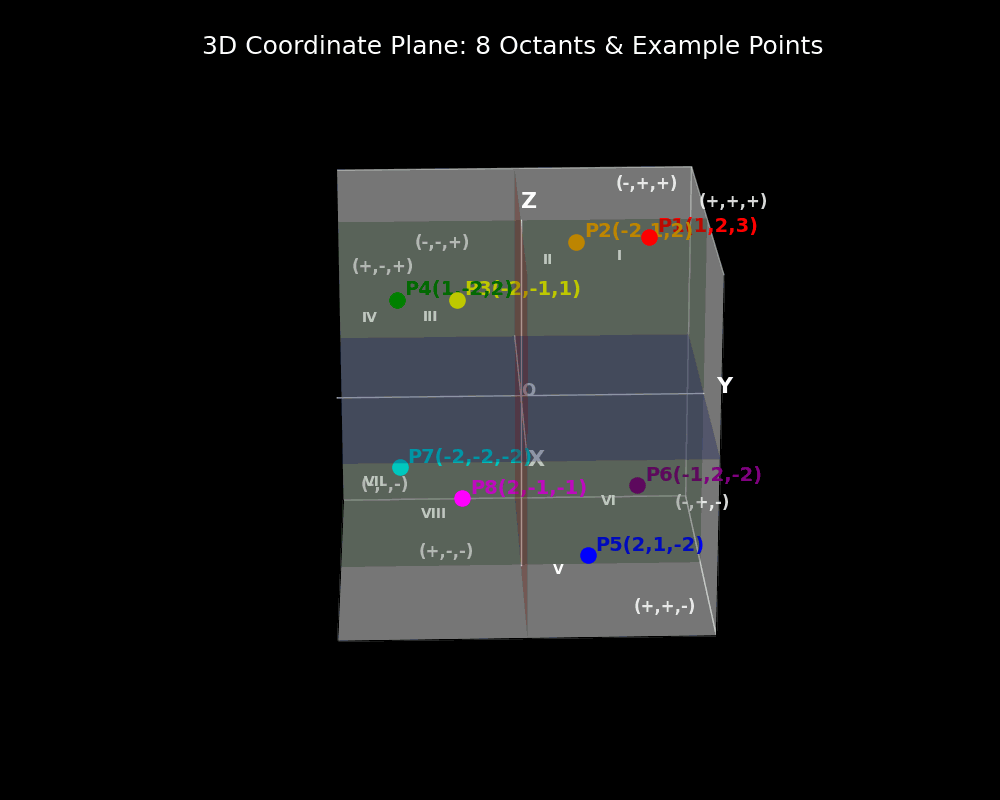
Unlike the two-dimensional plane, where the axes divide the plane into four quadrants, the three-dimensional Cartesian system divides space into eight regions, known as octants. Each octant is characterized by the sign (positive or negative) of the x, y, and z coordinates, allowing for the classification of points throughout the entire space. This organization facilitates the graphing of surfaces, solids, and spatial relationships, which is fundamental in fields such as geometry, calculus, physics, engineering, and computer graphics.

Here’s a visual representation of the eight octants in the three-dimensional Cartesian coordinate system, showing the placement of the x, y, and z axes, the origin, and the division of space into octants. Each octant is determined by the signs (+ or –) of the x, y, and z coordinates.

The general labeling convention:

• Octant I: (+x, +y, +z)
• Octant II: (–x, +y, +z)
• Octant III: (–x, –y, +z)
• Octant IV: (+x, –y, +z)
• Octant V: (+x, +y, –z)
• Octant VI: (–x, +y, –z)
• Octant VII: (–x, –y, –z)
• Octant VIII: (+x, –y, –z)

Octant	Sign Convention
Octant I	(+x, +y, +z)
Octant II	(–x, +y, +z)
Octant III	(–x, –y, +z)
Octant IV	(+x, –y, +z)
Octant V	(+x, +y, –z)
Octant VI	(–x, +y, –z)
Octant VII	(–x, –y, –z)
Octant VIII	(+x, –y, –z)

Overall, the x-axis, y-axis, z-axis, and the resulting octants are essential components of the three-dimensional Cartesian coordinate system. Understanding these elements is vital for visualizing and solving problems involving relationships among variables in three-dimensional space, forming the basis for more advanced studies in mathematics and related disciplines.

Ordered Pairs: The Language of Coordinates

The Cartesian coordinate system is fundamentally based on the concept of ordered pairs, denoted as (x, y). Each ordered pair identifies a unique point within the two-dimensional Cartesian plane. In this system, the first element, x, represents the horizontal distance from the vertical axis, while the second element, y, indicates the vertical distance from the horizontal axis. Together, these components provide a precise location for points in relation to the origin, which is the point (0, 0) where both axes intersect.

To illustrate, consider the ordered pair (3, 4). In this case, starting from the origin, one would move three units to the right along the x-axis, and then four units up along the y-axis. The resulting point would lie in the first quadrant, where both x and y values are positive. Conversely, if presented with the ordered pair (-2, 5), the movement would initiate by going two units to the left on the x-axis before moving five units up on the y-axis, placing the point in the second quadrant where x is negative and y remains positive.

Understanding ordered pairs is crucial for accurately plotting points on the Cartesian plane. When presented with a set of coordinates, each pair equates to specific horizontal and vertical distances from the origin, enabling clear visual representation. This systematic method allows mathematicians, scientists, and engineers to convey complex information effectively. Furthermore, ordered pairs function not only in geometry but also in various applications like graphing functions, analyzing data sets, and solving equations. As such, mastering the concept of ordered pairs is essential for anyone engaged in fields that rely on mathematical principles.

Geometric Representations: Transitioning between Algebra and Geometry

The Cartesian coordinate system serves as a fundamental framework for linking algebra and geometry, thereby enriching our understanding of both disciplines. By plotting points within the two-dimensional plane defined by the x-axis and y-axis, geometric shapes can be represented algebraically through equations. For instance, the equation of a line in slope-intercept form is expressed as y = mx + b, where ‘m’ denotes the slope and ‘b’ represents the y-intercept. When graphed, this linear equation forms a straight line, illustrating a direct correlation between algebraic and geometric properties.

Furthermore, curves also demonstrate this intersection of algebra and geometry. Equations such as x² + y² = r² depict circles whose radius is denoted by ‘r.’ This equation highlights how the geometric representation of a circle is intrinsically linked to its algebraic formulation. As students transition between algebraic equations and geometric shapes, they gain a versatile approach to problem-solving. The Cartesian coordinate system not only enables a clearer visualization of geometric concepts but also provides an analytical method to derive key algebraic solutions.

In particular, understanding the Cartesian plane enhances the comprehension of various geometric transformations, such as translations, rotations, and reflections. For example, translating a point can be visualized as shifting its coordinates, leading to a corresponding change on the graph. Such transformations allow learners to explore complex geometric patterns while reinforcing their algebraic skills. By mastering these connections, students can appreciate the unity of mathematics, where algebraic equations and geometric figures coalesce, fostering a profound insight into mathematical relationships.

Linear Equations and Their Graphs

Linear equations play a pivotal role in the Cartesian coordinate system, serving as the mathematical representations that define lines within this plane. A linear equation typically takes the form of y = mx + b, where ‘m’ signifies the slope of the line, while ‘b’ denotes the y-intercept, the point at which the line intersects the y-axis. The slope indicates the steepness and direction of the line—positive slopes incline upwards, whereas negative slopes descend. Understanding this form allows for the visualization of linear equations as straight lines on the Cartesian plane.

To sketch the graph of a linear equation, one can identify critical points by substituting values for ‘x’, thus calculating corresponding ‘y’ values. For instance, substituting x = 0 into the equation yields the y-intercept, while substituting x = 1 or x = -1 provide additional coordinates. Plotting these points on the Cartesian grid and connecting them will illustrate the straight line represented by the equation.

Finding coordinates of points on the line is essential not only for graphing but also for understanding relationships between variables. For example, let’s consider the linear equation y = 2x + 3. Plugging in x = 1 results in y = 5; hence, the point (1, 5) is plotted on the graph. Continuing this process for various x values will yield multiple coordinates, allowing one to observe the linearity and predict further points along the line. This method of solving linear equations enhances comprehension of how changes in one variable directly influence another in a linear relationship.

In conclusion, mastering linear equations and their graphical representation is crucial for utilizing the Cartesian coordinate system effectively. Understanding how to derive points from equations aids in recognizing the broader implications of linear relationships in various mathematical applications.

Understanding Functions through Graphs

The representation of functions in the Cartesian coordinate system is fundamental for analyzing mathematical relationships. Functions are essentially mappings from a set of inputs, known as the independent variable, to a set of outputs, referred to as the dependent variable. Each input corresponds to a unique output, which can be expressed in the form of an ordered pair (x, y), where ‘x’ represents the independent variable, and ‘y’ is the dependent variable derived from the function.

Developing a comprehensive understanding of how to graph functions is critical in visualizing the relationship between these input-output pairs. The Cartesian coordinate system uses two perpendicular axes: the x-axis for the independent variable and the y-axis for the dependent variable. When graphing a function, each ordered pair is plotted on this grid, allowing us to observe patterns and behaviors of the function. For instance, the shape of the graph can indicate whether the function is linear, quadratic, or follows a different pattern altogether.

Visualizing functions through graphs offers several advantages. Firstly, it provides an intuitive understanding of the behavior of a function. For example, a linear function will produce a straight line, while a quadratic function creates a parabolic curve. By plotting multiple points, one can see how the function behaves across different ranges of the input variable. This visualization aids in recognizing key features such as intercepts, maxima, minima, and asymptotes, which are crucial in many areas of mathematics and applied sciences.

Furthermore, understanding functions through their graphical representation enhances problem-solving skills. Having a visual reference allows mathematicians and scientists to make predictions about the function’s behavior and offers insights into the relationships among various inputs. Thus, apprehending functions within the Cartesian coordinate system serves not only as a mathematical exercise but also as a foundational skill in the broader scientific discourse.

Applications in Various Fields

The Cartesian coordinate system serves as a foundational concept that extends its influence across multiple domains, including physics, engineering, and computer graphics. In physics, this system is instrumental for graphing motion and forces, allowing for the precise representation of physical phenomena. For instance, when analyzing projectile motion, the coordinates can be utilized to illustrate the trajectory of an object, enabling physicists to predict its path and calculate relevant parameters such as velocity and acceleration. This application significantly aids in understanding fundamental principles of kinematics.

In engineering, the Cartesian coordinate system provides a robust framework for design and analysis. It is crucial in fields like civil and mechanical engineering, where structures and machines are modeled using rigorous geometric representations. Engineers use the coordinate plane to draft blueprints and schematics, allowing them to visualize and manipulate components precisely. The concept of coordinates also underpins stress analysis, where graphing forces on structures aids engineers in ensuring safety and functionality.

Furthermore, the influence of the Cartesian coordinate system is profoundly felt in computer graphics. This field relies heavily on 2D and 3D coordinate systems for rendering images and creating visually immersive environments. For example, in video game development, objects are positioned, transformed, and animated within a Cartesian framework, which facilitates real-time rendering and interaction. The application of the coordinate system in graphic design, animation, and simulation not only enhances visual clarity but also optimizes the efficiency of computational processes.

In conclusion, the Cartesian coordinate system is more than an abstract mathematical concept; it is a practical and essential tool that finds extensive applications in various fields. Its versatility underscores its significance in solving real-world problems, demonstrating its relevance across multiple disciplines.

Advantages of the Cartesian Coordinate System

The Cartesian coordinate system offers several advantages that make it a crucial tool in various fields of mathematics, particularly in geometry and algebra. One of the primary benefits of using this system is its simplicity and effectiveness in problem-solving. By providing a clear and distinct framework for representing points in a two-dimensional or three-dimensional space, the Cartesian system simplifies the process of analyzing geometric shapes and equations. For instance, plotting linear equations on a graph helps students visualize the relationships between variables and enhances their understanding of slopes and intercepts.

Furthermore, the Cartesian coordinate system makes the visualization of complex concepts significantly easier. With the ability to represent mathematical relationships graphically, learners can better grasp difficult ideas such as transformations, intersections, and distance. For example, the ability to see how changes in one variable impact another through graphical representation can clarify the concept of functions, allowing students to develop a more intuitive understanding of mathematics.

Additionally, the Cartesian coordinate system serves as a foundational tool for advanced mathematics. Many higher-level mathematical concepts, including calculus, statistics, and linear algebra, rely on an understanding of coordinate systems to analyze data and functions effectively. As students progress in their studies, a solid grasp of the Cartesian plane becomes essential for tackling more intricate mathematical problems and for applications in physics and engineering.

In summary, the advantages of the Cartesian coordinate system lie in its capacity to simplify problem-solving processes, facilitate visualization of complex mathematical concepts, and lay the groundwork for more advanced studies. By integrating these aspects into mathematics education, learners can build a stronger understanding and appreciation for the subject as a whole.

Summary

The Cartesian coordinate system, named after the French mathematician René Descartes, has profoundly influenced mathematics and its applications since its inception. This innovative framework allows for the precise representation of geometric figures and the relationships between them in a two-dimensional or three-dimensional space. By integrating algebra and geometry, the Cartesian system establishes a nexus that enables mathematicians to describe complex shapes, trajectories, and graphs more effectively.

Significantly, the adoption of the Cartesian coordinate system has transformed various fields, from engineering to physics and even computer science. In engineering, for instance, the ability to map out designs accurately has streamlined the manufacturing process. In physics, the Cartesian system facilitates the analysis of motion and force through vector representation, aiding scientists in making predictive calculations about physical phenomena. Moreover, in computer science, algorithms that rely on geometric computations heavily utilize Cartesian coordinates to optimize graphical rendering and data visualization.

Furthermore, the importance of the Cartesian coordinate system extends beyond traditional mathematics and the sciences. It serves as a foundational concept for various mathematical disciplines, including calculus, linear algebra, and topology. Mastery of Cartesian coordinates is essential for students engaging in these advanced topics, as it equips them with tools to interpret and analyze mathematical relationships more deeply. Understanding this system not only fosters mathematical reasoning but also cultivates critical thinking skills applicable across diverse domains.

In conclusion, the Cartesian coordinate system remains a cornerstone of modern mathematics and its interconnected applications. Its lasting legacy underscores the necessity of grasping this fundamental concept for anyone pursuing studies in mathematics or related areas. As learners continue to explore and apply the Cartesian coordinates, they are ultimately engaging with a pivotal element that has shaped numerous disciplines through the centuries.