Conic Sections: The Geometry of Curved Beauty

Conic sections, also known as quadric curves, are fundamental geometric shapes that arise from the intersection of a plane and a cone. These curves, including the ellipse, parabola, and hyperbola (with the circle as a special case of the ellipse), have captivated mathematicians and scientists for centuries. Their elegant properties and diverse applications in fields like physics, astronomy, and engineering make them a cornerstone of mathematical understanding. Their diverse properties and applications continue to fascinate and inspire, demonstrating the enduring power of mathematical exploration. The following sections will delve deeper into the fascinating world of conic sections, exploring their origins, characteristics, and significance.

So, let’s get started and discover the elegance of Conic Sections , their diverse forms, and the practical applications that make them so essential. We’ll see how these curves, initially studied by ancient Greeks, continue to shape our understanding of the world around us.

Furthermore, as we continue with Conic Sections, we’ll also examine the algebraic representations of these curves, delving into their equations and properties. We’ll learn how to classify them using discriminants and explore their standard forms. We’ll look at how they’re defined by their equations, and how their properties influence the orbits of planets, the design of telescopes, and the structure of bridges. Moreover, you’ll see how these concepts apply to real-world scenarios. Whether you’re a student, a math enthusiast, or simply curious, this exploration of Conic Sections will provide you with a solid foundation in this important area of geometry.

---

---

Understanding Conic Sections and Their Definitions

Conic sections are traditionally defined as the curves formed by the intersection of a plane and a double cone. The nature of the resulting curve depends on the angle at which the plane intersects the cone.

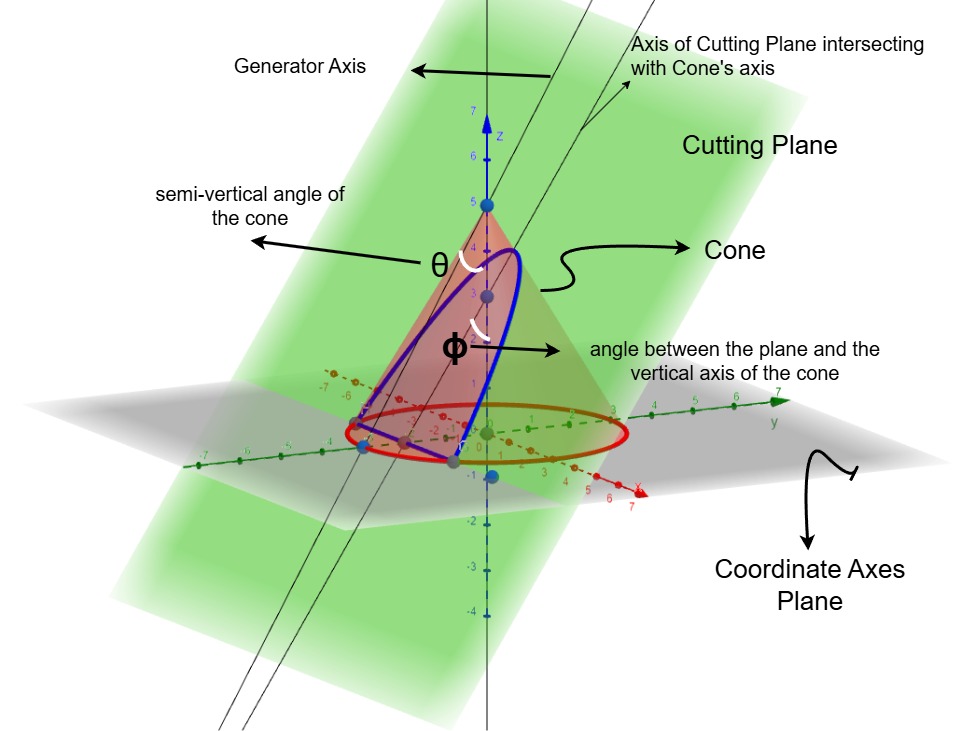
If the plane cuts entirely through one nappe of the cone without intersecting the vertex, the result is an ellipse. When the plane is parallel to a single generating line of the cone, the intersection is a parabola, an unbounded curve. Finally, if the plane intersects both nappes of the cone, the result is a hyperbola, which consists of two separate unbounded curves. The circle, a special case of the ellipse, is formed when the plane intersects the cone perpendicularly to its axis. This geometric definition provides a visual and intuitive understanding of how these curves are generated. The Conic Sections are a rich source of geometric properties.

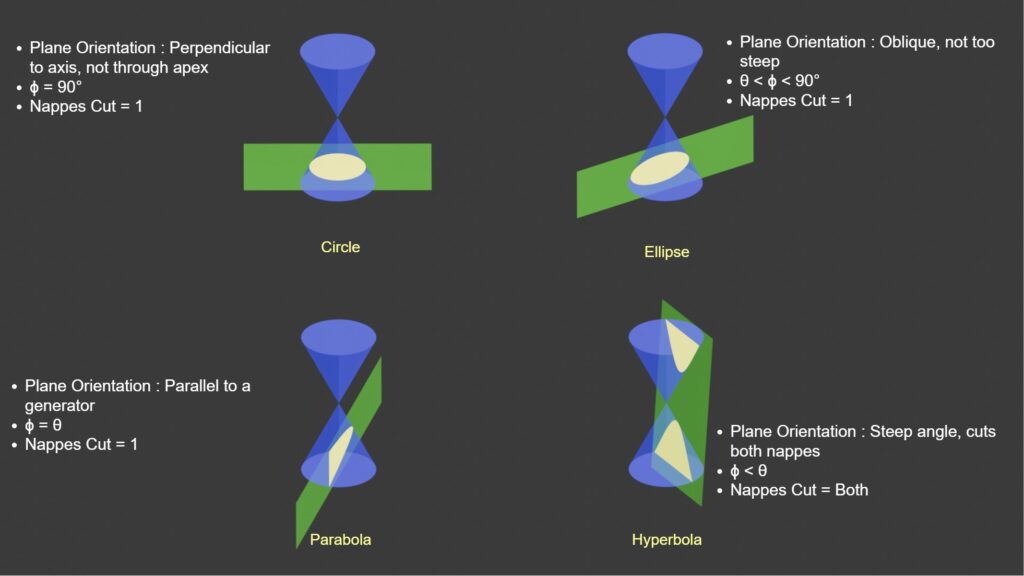
Conic Section	Plane Orientation	Condition (Angle Relation)
Circle	Perpendicular to cone’s axis, intersects one nappe	φ = 90°
Ellipse	Oblique, intersects one nappe	θ < φ < 90°
Parabola	Plane is parallel to a generator of the cone	φ = θ
Hyperbola	Oblique, intersects both nappes	φ < θ

Alternative Definitions and Properties

Conic sections can also be defined using the focus-directrix property. This definition states that

A conic section is the set of all points where the ratio of the distance to a fixed point (the focus) and the distance to a fixed line (the directrix) is constant.

This constant ratio is called the eccentricity, denoted by e. If e is less than 1, the conic is an ellipse; if e equals 1, it’s a parabola; and if e is greater than 1, it’s a hyperbola. The circle, in this context, is a special case where the eccentricity is zero, and the directrix is considered to be at infinity.

This focus-directrix definition provides an alternative way to understand and characterize these curves, highlighting their fundamental geometric relationships. This definition is very important in understanding the various properties of Conic Sections.

The Projective Plane and the Unified View of Conic Sections

While the Euclidean plane presents conic sections as distinct entities, a more unified perspective emerges when considering the real projective plane. In projective geometry, the apparent differences between the ellipse, parabola, and hyperbola vanish, revealing a deeper connection. The real projective plane is constructed by adding a “line at infinity” to the Euclidean plane, where parallel lines are considered to meet. This addition allows us to view the parabola as a closed curve, with its ends meeting at a point on the line at infinity. The hyperbola also becomes a closed curve, with its two branches intersecting at two points on the line at infinity. The ellipse remains a closed curve, but its relationship to the other conics becomes more apparent in this unified framework. This perspective simplifies the classification of conic sections, as all non-degenerate conics become equivalent under projective transformations. This means that any conic can be transformed into any other conic through a suitable projective mapping, highlighting their fundamental similarities.

In the projective plane, the equation of a conic section takes the form

###Ax^2 + Bxy + Cy^2 + Dxz + Eyz + Fz^2 = 0###

where the introduction of the homogeneous coordinate z allows us to represent points at infinity. This equation encapsulates all types of conics, and their classification depends on how they intersect the line at infinity. The type of conic is determined by how the conic intersects the line at infinity. The three types are then determined by how this line at infinity intersects the conic in the projective space. In the corresponding affine space, one obtains an ellipse if the conic does not intersect the line at infinity, a parabola if the conic intersects the line at infinity in one double point corresponding to the axis, and a hyperbola if the conic intersects the line at infinity in two points corresponding to the asymptotes. This approach provides a powerful tool for studying the properties of conic sections and their relationships. The projective view not only unifies the different types of conics but also simplifies many proofs and calculations. It offers a more profound understanding of these shapes and their place in the broader landscape of geometry.

Solving the Problem: Equations and Properties

In analytic geometry, conic sections are represented by quadratic equations in two variables. The general form of such an equation is ##Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0##, where A, B, C, D, E, and F are constants, and A, B, and C are not all zero. The coefficients A, B, and C determine the type of conic section. The discriminant, calculated as ##B^2 – 4AC##, provides a straightforward way to classify the conic: if it’s less than zero, the conic is an ellipse (or a circle if A=C and B=0); if it equals zero, it’s a parabola; and if it’s greater than zero, it’s a hyperbola. This algebraic representation allows us to analyze and manipulate conic sections using the tools of algebra and calculus. Understanding these equations is crucial for solving problems related to Conic Sections.

Standard Forms and Parametric Equations

Conic sections can be expressed in standard forms, which simplify their analysis. For example, the standard form of an ellipse centered at the origin with semi-major axis a and semi-minor axis b is ##\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1##. The standard form of a parabola with its vertex at the origin and focus on the x-axis is ##y^2 = 4ax##. The standard form of a hyperbola centered at the origin with a horizontal transverse axis is ##\frac{x^2}{a^2} – \frac{y^2}{b^2} = 1##. These standard forms are derived through transformations (rotations and translations) of the general quadratic equation. Additionally, conic sections can be represented parametrically. For example, an ellipse can be described by the parametric equations ##x = a \cos(\theta)## and ##y = b \sin(\theta)##, where ##\theta## is a parameter. These parametric equations are useful for tracing the curve and calculating various properties, such as the area enclosed by the ellipse. This allows us to delve into the world of Conic Sections with greater precision.

The Essence of Conic Sections: A Historical Perspective

The genesis of conic sections can be traced back to ancient Greece, where mathematicians like Menaechmus and Euclid first explored these intriguing curves. However, it was Apollonius of Perga, around 200 BC, who truly systematized their study in his seminal work, “Conic Sections.” Apollonius not only defined the ellipse, parabola, and hyperbola but also investigated their properties in remarkable detail. His contributions laid the groundwork for future generations of mathematicians and scientists. The Greeks initially defined conic sections by intersecting a plane with a cone. This early definition, while fundamental, was later augmented by the focus-directrix property, which provided an alternative way to characterize these curves. This property, which defines a conic as the locus of points whose distances to a focus and a directrix are in a fixed ratio, offered a new perspective on these shapes and paved the way for their algebraic representation.

The study of conic sections during the Hellenistic period was not merely an academic exercise; it was deeply intertwined with practical applications. Archimedes, for instance, used parabolas to calculate areas and volumes, showcasing the potential of these curves in solving real-world problems. The work of Apollonius, however, went far beyond practical applications. He delved into the intricate properties of these curves, exploring their tangents, normals, and other geometric features. His systematic approach and rigorous proofs established a foundation for the development of analytic geometry centuries later. The legacy of these early mathematicians is evident in the enduring presence of conic sections in modern mathematics and science. Their contributions, which provided the basis for understanding these fundamental shapes, are still relevant today, and their influence can be seen in various fields, including optics, astronomy, and engineering.

Conic sections have numerous applications in various fields. In astronomy, the orbits of planets and comets around the sun are conic sections, primarily ellipses. The reflective properties of conic sections are utilized in the design of telescopes, antennas, and searchlights. Parabolic mirrors focus parallel rays of light or radio waves to a single point, while hyperbolic mirrors are used in telescopes to reflect light to a focus. The study of conic sections dates back to ancient Greece, with mathematicians like Menaechmus, Euclid, and Archimedes making significant contributions. Apollonius of Perga, in the 3rd century BC, wrote a comprehensive treatise on conic sections, which became a standard reference for centuries. His work systematized the study of these curves, providing detailed analyses of their properties and relationships. The historical context of Conic Sections is fascinating.

Modern Relevance

The development of analytic geometry by René Descartes and Pierre de Fermat in the 17th century revolutionized the study of conic sections. By introducing coordinate systems, they transformed geometric problems into algebraic ones, making it easier to analyze and solve them. This approach led to the derivation of the standard equations and the development of powerful techniques for studying these curves. Today, conic sections continue to be a fundamental part of mathematics education and are essential for understanding various scientific and engineering principles. Their applications extend to areas like computer graphics, where they are used to create realistic curves and surfaces. The legacy of Conic Sections continues to shape our understanding of the world.

Problems on Conic Sections

Problem 1: Identify the conic section represented by ##x^2 + y^2 = 25##

This is a circle with radius 5.

Problem 2: Determine the type of conic section for ##y^2 – 4x – 4 = 0##

This is a parabola.

Problem 3: Find the eccentricity of the ellipse ##\frac{x^2}{9} + \frac{y^2}{4} = 1##

Eccentricity is ##\frac{\sqrt{9-4}}{3} = \frac{\sqrt{5}}{3}##.

Problem 4: Write the equation of a hyperbola with vertices at (±3, 0) and foci at (±5, 0)

The equation is ##\frac{x^2}{9} – \frac{y^2}{16} = 1##.

Problem 5: What is the focus of the parabola ##y^2 = 8x##?

The focus is at (2, 0).

---

---